Metaphor as a Way Out

An Intuitive Introduction to Intentional Evolution

Metaphor is a new path towards Artificial General Intelligence (AGI, though Universal Intelligence is the more apt term, as we’ll see). By formalizing the notion of analogy, Metaphor allows us to build systems that are well-positioned to withstand, adapt, predict, and explain change in dynamical environments filled with unforeseen events and unknown unknowns. These systems can learn using both the gradual local optimization that perfects an automation and the serendipitous leaps and bounds of discovery and imagination.

We sketch here, using a first-principles approach, the inherent limits of our current efforts in Machine Learning, and rephrase the problem so that a natural way forward appears. We then describe the practical details, applications, and implications of using Metaphor as a paradigm and workflow for Universal Intelligence research and development.

While the subject is complex and the arguments technical we favor a more intuitive and visual approach, with few code snippets or equations involved.

The Four Kinds of Problems

One way to think about the kinds of problems we’re facing in our day-to-day and professional lives is to classify them based on our knowledge of our knowledge. Put in another, less mind-bending and tongue-twisting way: What do we need to teach someone else for them to be able to solve the problem? This neatly categorizes any problem to one of four possible types.

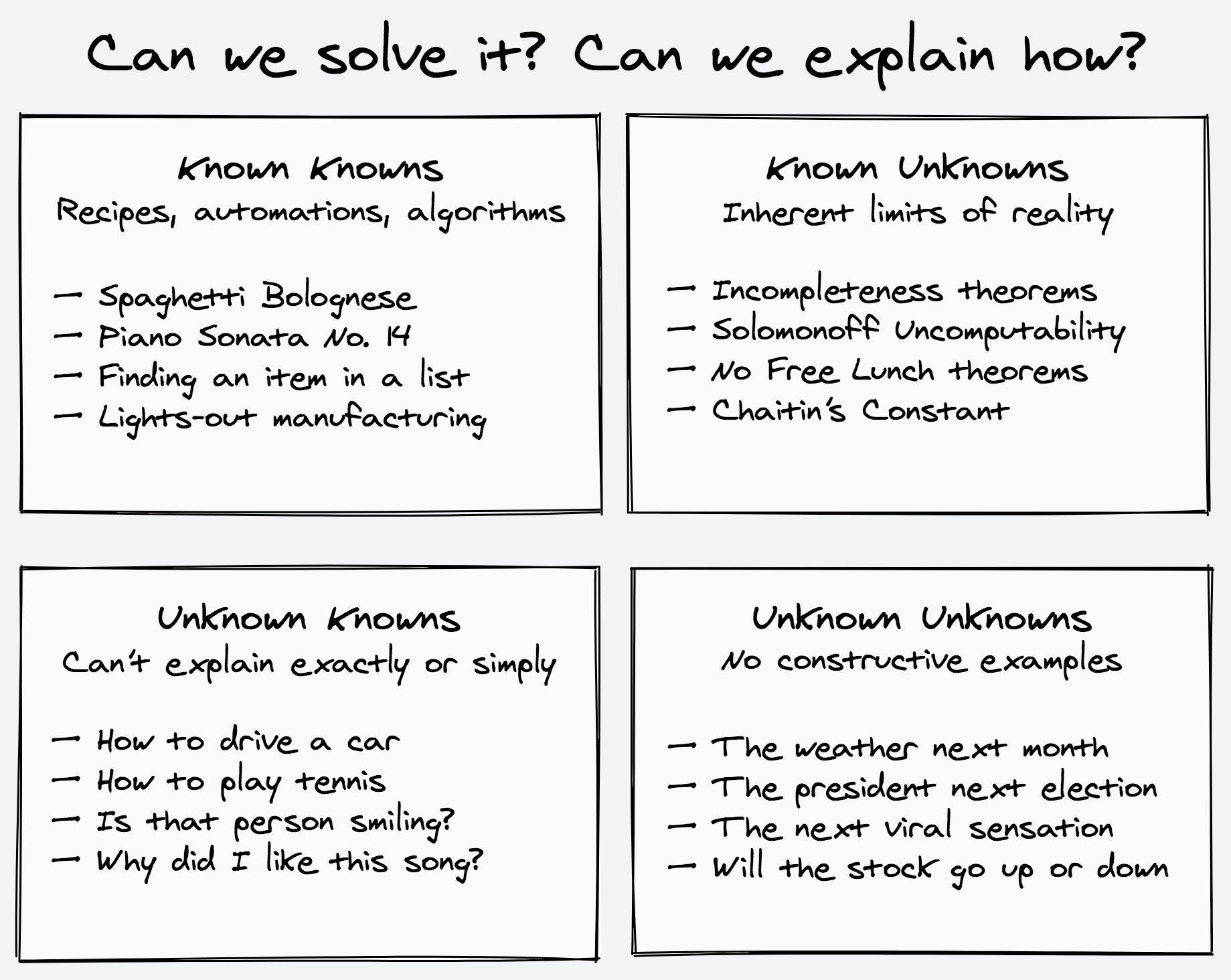
The Known Knowns are the things we know how to solve and exactly how we’re solving them. These problems can be reduced to parts and automated as factories, recipes, and algorithms. The solutions are straightforward, even if sometimes finicky and exacting. They lend themselves to mnemonical, atomic, modularized forms. They are what we hope to arrive at, so that we can give the keys to a well-oiled machine and continue with the more interesting parts of our lives.

The Known Unknowns are the things we know will forever be out of reach. These are the inherent limits, difficulties, and impossibilities of physical, mathematical, and computational reality — the Bekenstein bound, Gödel’s incompleteness theorems, and computational complexity separations are just some of the results that perpetually obstruct our way. We can only accept them and work around them.

The Unknown Knowns, or I know it when I see it, are the things we do know how to solve, but not exactly sure how we’re doing so. These are problems of both high-level subjective and cultivated taste and low-level sensor and motor skills — picking the right song for the mood, the right word for a sentence, the right color for a painting, or reading facial expressions, sensing if a pause is for thought or a space for response, navigating in a packed crowd, and so on. The doors leading to the engine room of the mechanics involved seem barred to us. We can only observe and test them indirectly and from the outside, through specific examples.

Trying to outline these problems we see our pen taking many turns. There’s a lot of ifs and buts and not necessarilies and sometimes, and always there’s those pesky special cases, a slight resemblance of sorts, and tiny critical details preventing any kind of elegance from forming. These problems refuse to submit to a digestible explanation, a clear story, a categorization that can be easily shelved and retrieved, a napkin calculation, or an equation we can do in our heads. They are not succinct nor simple to describe.

Up until recently the Unknown Knowns were the prerogative of humans, laborers and curators alike. Machine Learning has made it possible for computers to carve their own niche here using universal function approximators. With enough labeled examples and computational capacity there’s no such task we cannot automate an imitation of: collect a list of what’s this and what’s that, sketch some border lines to divide at random, and start moving the lines around — squeezing, scaling, rotating, smoothing, and bending — progressively getting a better approximation, a tighter shape around what we already know.

Can this process of automation based on past experience capture some of the things we don’t already know, shed light on unseen variations, hidden explanations, and rare combinations? Sometimes it can. But there’s no guarantee that everything or anything new or unexpected will be found out, or that its static extrapolations and reactive predictions will even keep up and continue to be in accordance with reality.

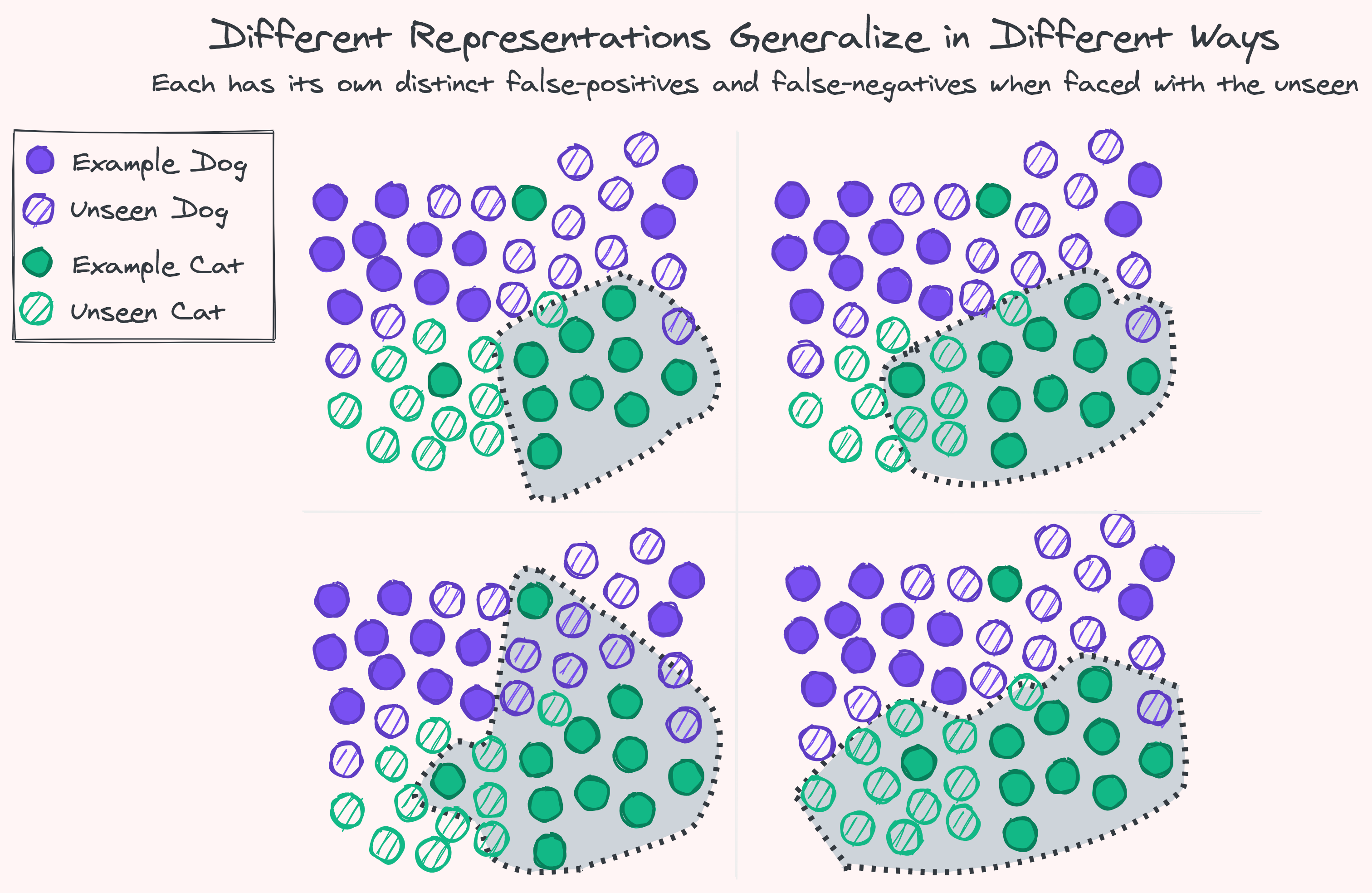
The Unknown Unknowns are the things we don’t even know if we could ever know, the things we can’t even give an example of. By the sheer act of thinking about them we give them form and make them known, expected, and imaginable. There is no specific constructive instance to point at. The specifics of the unknown can only be talked about subjectively and rationalized in hindsight. Any instance you find has already moved to being known.

Yet there is always a constant stream of startlingly fresh unknown unknowns. Even though most will forever remain so — we’ll never be aware of their existence, let alone solve them — some will eventually be discovered. We’ll get to know them, get to have a feeling of what is and what isn’t about them, and, in time, articulate the why and automate the how.

As we better our grasp, the instances we encounter move toward the knowable end of the continuum, yet their class can remain an everlasting source of new experiences. There will always be new clichés. There will be no end to slang and jargon that makes people feel old and confused. Always new ways for people to express themselves. New stories to tell, new art to inspire, new music to touch. We will always have new mathematical truths and proofs to discover, though our worldview is now clear on some theorems which stumped the brightest of minds for centuries.

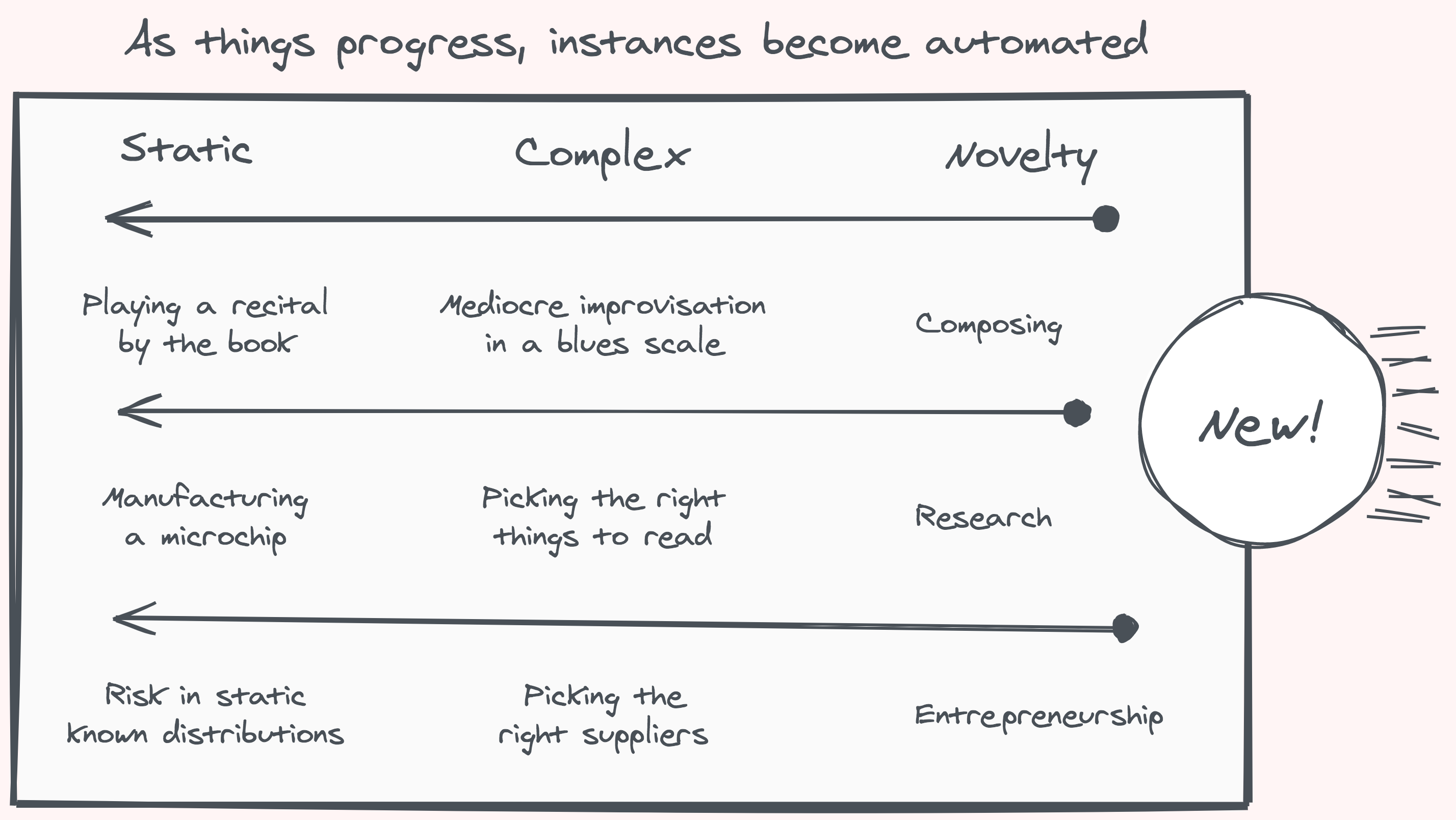
The unknown unknowns are hard to find but can be easy to learn. We can hardly imagine how unobvious these things were, how much skill and perseverance were involved in figuring them out. It took generations of brilliant effort to come up with the things we now expect high schoolers to master. We ask ourselves how we could not foresee the now-so-obvious market bubble or the second-order effects of a foreign policy yet we forget, among many such examples, that the concept of a sandwich hadn’t quite entered the European mind before the eighteenth century.

The Frontier of the New

So far, the unknown unknowns have only been tackled successfully by evolutionary forces and the human mind, using insight and serendipity. The separation, where our methods of automation fail, and only mind and life succeed, is at the frontier of the new. Here, the unexpected is a recurring theme, and there’s no hope in imitation, whether it mimics a static pose or a vector of motion: following a path is not charting a course. Imitation might be good enough, until it isn’t.

It is important to remember that, on the more comfortable side of the line, where things are known, there is no point to flair, invention, and exploration, as all you need to do once found is follow the recorded steps. Over time, for any specific thing, automation always wins. That’s what we want. If you already perfectly know what you’re doing, what’s the point of doing it?

To try a definition and mark the border: what’s new, to us, is what we can’t ever think about as a whole, no matter how much we try. What can never be compressed to fit our size. If we can’t predict (or memorize) what’s a process going to do next — in less time and space than it takes the process to do so — then parts of it will forever be new to us.

Any given model, no matter its size, will always have new things relative to it, things it cannot encompass perfectly. This is not a new result. Many of the limits to knowledge we’ve discovered in the past century directly address this issue. Yet we continue to break our heads against this wall, hoping against hope it would crack. Why can’t our methods of optimization take on the new? Two critical obstacles, inherent to their nature as static goal-seeking algorithms, block their path.

Two Jews, Three Opinions: Choosing Hypotheses

In an unknown universe, it is often impossible to pick a single way forward. Many theories and hypotheses can explain a situation, and there is not enough evidence to risk it all on one. What can we do when we must choose?

Occam’s Razor is only a rule of thumb, not a law. Even if we could correctly quantify the simplicity of each explanation, there is no guarantee that the more complex explanation is not the right one, that further evidence will not invalidate the simpler explanation. What is the next number in the series 1, 1, 2, 3, 5, 8, …? It’s -75.32. Why? Because. Maybe saying 13 is the best decision that a single rational agent can take with its limited capacity in this world. We can’t fault the agent for that, but we can blame ourselves for not creating a robust system that supports multiple approaches.

On the other hand, “if more than one theory is consistent with the observations, keep all such theories” is also an impossible advice to follow in practice as enumerating all possible theories is usually uncomputable or at best infeasible.

Further, if our explanations take an active part in the world, they will have the hopeless task of perfectly accounting for their own decisions and actions in their decisions and actions, an infinite regress.

Even if we could see all options, theories, and suggestions, and have vast ensembles of experts weigh in on each solution, our world is still non-ergodic. It still demands individual action — there are now-or-never situations that only allow for a single choice to be taken. We can’t try again and again. As we have limited resources and visibility we must gamble, and hope our conviction aligns with reality.

If You Meet the Buddha on the Road, Kill Him

The final blow to our optimization efforts holds the most irony and presents their futility bare. It is their own goal-seeking that leads to their downfall. Optimization is its own Achilles’ heel. Some reflections of the possible answers are always alluded to by the question. The only way to seek anything is to look for nothing.

Seeking requires a rule of movement, a heuristic acting as a proxy for what we expect to find. As the proxy can only mirror incomplete aspects of the real thing — for otherwise we would already know that which we are after — an adversary can exploit this separation and lead us astray. So long as there even a miniscule disconnect between the rule of thumb and the reality it reflects — and there always has to be one — an optimization can be pushed to blindly follow a path toward inhospitable corners of the hypothesis space.

For example, imagine a group of explorers intent on finding the lowest valley by way of looking closely around and walking in the direction of the steepest decline. It’s not hard to construct an environment that will fool and trap them in a very benign location, far away from their true goal. No matter what guides you — so long as it’s not an exact copy of the answer — the difference can be exploited to lock the you from getting anywhere worthy in any reasonable amount of time.

This is like a game of 20 questions where your opponent gets to hear your questioning plan before picking a person to think of. Even if you’ve devised the perfect questions to separate the population to equal halves at every step, you’ll still only be able to pinpoint around a million (2²⁰) people — much less than the number of personalities on, say, IMDB. Whatever strategy you choose, whatever assumptions you hold, there will be ample counterexamples for your adversary to stump you with.

We’re now left only with methods that do not try to exploit the assumed structure of the problem, that do not have any prior bias to what they are looking for or how they’re looking for it, since any such predisposition can be used against them. One approach is to comb through all possibilities at random, hoping by some miraculous fluctuation to arrive at a Boltzmann Brain. Another, as exemplified by AIXI, is to enumerate through them all in some methodical, brute-force fashion. Both are impractical and intractable.

If there is no problem-specific structure we’re allowed to rely on, the only thing left to use is the structure of information itself.

Making an Analogy

In light of the limitations of the new and the unknown, let us restate our goals in less ambitious terms. We’re looking for simple structures to help us navigate and make sense of the complexities of the world — compressed, succinct programs that expand to encompass many related situations. We do not aim to tame the vast majority of phenomena — it is too nuanced to comprehend — only some bits and pieces, the small isolated islands that offer explanations to more than themselves.

This offers a view to the unreasonable effectiveness of mathematics. The study and surveying of abstract structures is crucial not because the world is necessarily filled with beautiful patterns and hidden symmetries, but because the ordered and the simple are the only things we can latch and hold onto in a tumultuous sea of possibilities. Are there any rules to the universe that require 10¹⁰⁰ bits to define? Maybe, but we’ll never have the capacity to use them, much less the ability to discover them. We’re then left with a more modest group of truths we can grasp and practically use.

Yet even within our reach, simple explanations — the compressed programs that can succinctly capture many facets of reality — are hard to find. They are few and far between. This is not just our impression; Algorithmic Information Theory codifies this: there are simply not enough small programs to capture all the possible variations of information. Yet there is a shortcut, a vein we can tap, a high-level space that connects groups of explanations, and groups of groups, in a loose network of compact theories.

Analogies are at the core of life and cognition. They offer us a way to break free from the chains of the known and nearby and take leaps of imaginations to faraway, opposite, and contradictory vistas. These forays are not random wild guesses — they take the heart of the matter and look at it from a different angle.

It may sound counterintuitive to look at exactly the things that capture most of what we’re doing now — and doing well enough to exist — and think that this is the right place to start shaking the system from. But where else? Imagination is not random, it needs something to run with, and these are exactly the elements we can use to form a language for the situation we find ourselves in. When we are able to describe a structure succinctly we form a higher-level representation, a language that allows us to explore alternatives. By defining exactly what is at the core of a pattern, we can look at its opposites. And these counterfactuals will also be succinct and compact explanations — a very rare thing, and exactly what we’re looking for.

Take, for example, the binary string:

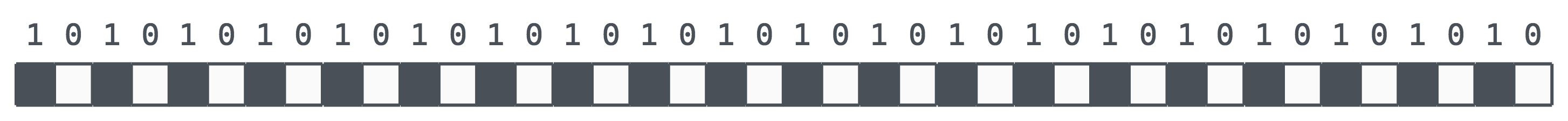
It can be described succinctly and represented in several different ways. One is: print ‘\(10\)’ twenty times repeatedly. Another: print ‘\(1010\)’ ten times. Yet another: print the previous bit, flipped, forty times, starting with one. It can also be described just as-is: one then zero then one then zero, and so on.

Let’s look at a few possible one- or two-bit mutations to the full unrolled bit pattern description:

Not much to report. Small wiggles and wobbles of noise here and there. How would you relate these patterns to another person? For instance, we might describe the last ‘like a checkered pattern, but with three white dots in a row somewhat in the middle, and two black dots at the end’. It’s not much for conciseness.

Now we’ll try the same one- and two-bit mutations using one possible compressed representation of the string. We’ll use the first five bits to declare how many times we want to print the string (up to 32 times) and the rest to describe the pattern we want printed multiple times. Note that in this scheme we can represent our bit pattern in six different ways. We’ll choose as our baseline representation to print the string \(1010\) ten times.

Much more interesting patterns this time around, ones that are much easier to describe to someone else. As we’re using 9 hyperbits, this representation scheme offers us access to 2⁹ (= 512) different compact programs, ignoring a few edge cases where a hyperbit controls only one output bit, and some overlapping representations that share the same output. The number of compressed programs we can find grows exponentially with the number of hyperbits that we have.

We can compare the expressibility of different analogy spaces, quantify the mutual-information and range of effect of each hyperbit, and measure the distance between different programs in an analogy space. To get from our baseline representation to a flipped one — a checkered pattern of \(0101\ldots\) — we’ll need to flip four bits. From a representation that prints \(10\) twenty times it only takes two bit flips to get there. From a representation that zigzags between on/off it can just be a single bit, like a piano designed specifically for two songs. In the original unrolled description it would take 40 bit flips to perfectly align together, a chance of about one in a trillion.

Analogies as a Hedge Against Change

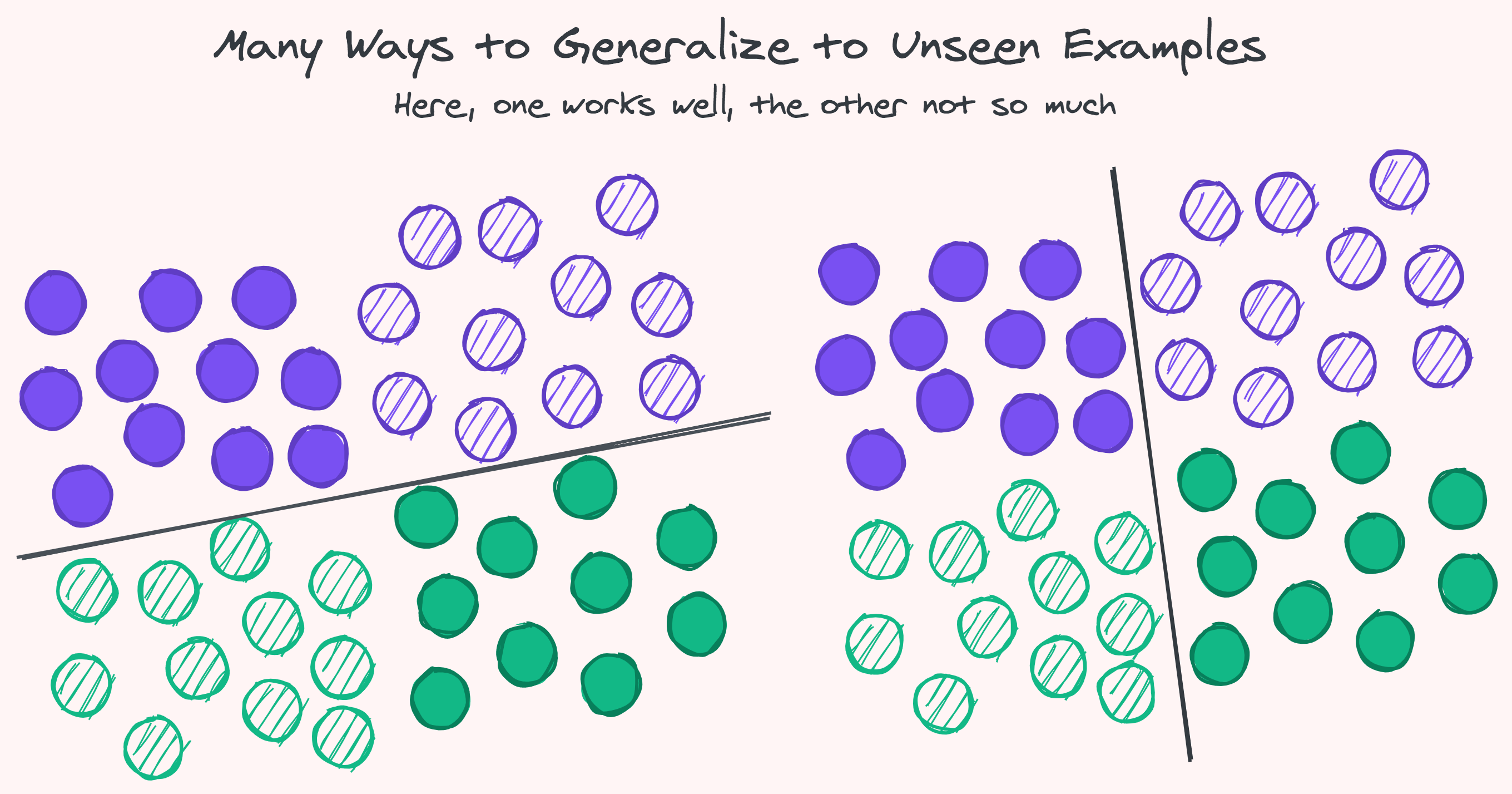
Let’s see how analogies fare in a simple scenario. In the following 2D dynamic fitness landscape the goal of the agents is to find the red-hot zone. On the left we have a group of agents using a method called Evolutionary Strategy (ES), that, at scale, approximates the gradient descent used in deep learning methods. On the right we have agents that use Metaphor’s approach — they work independently, take analogical leaps, and are able to quickly adapt as the landscape changes.

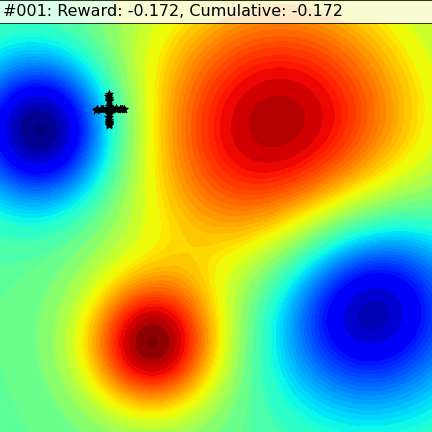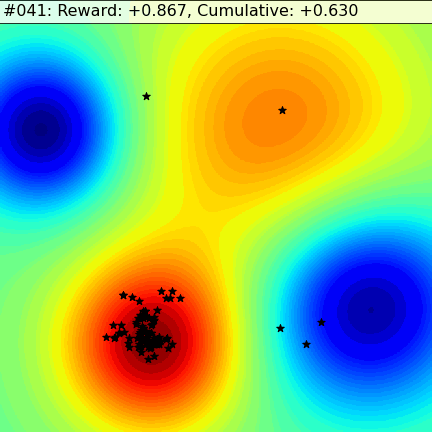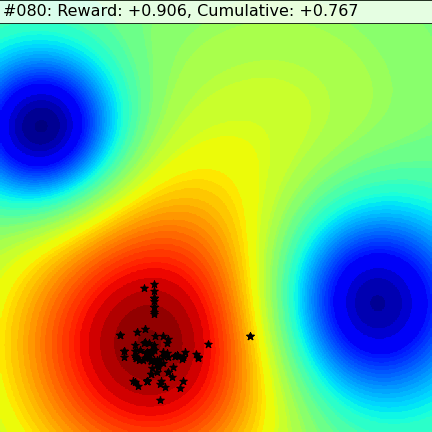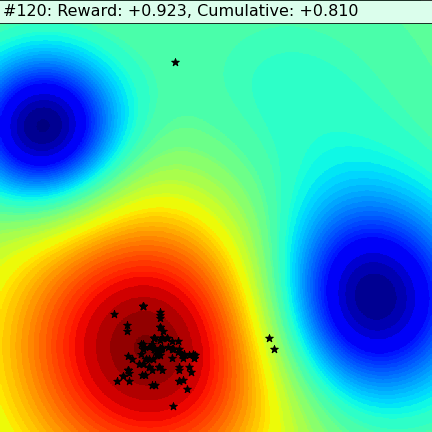
The ES agents use local optimization: they flutter around in their close neighborhood, at each step trying to find a slightly better spot, finding their way to the center of the nearest minima. But, as it diminishes, they sit idly by, unable to see any alternative to migrate to. Only when the minima evaporates completely do they start moving to the other one.

Metaphor’s agents use analogies as escape hatches. This allows them to quickly discover the two minima, maintain a colony in both, and quickly migrate over before a catastrophe engulfs them. As the time comes to generate a new set of explanations whoever sits on a more comfortable red-hot zone gets a larger slice of the pie, a larger chance to influence the offspring. Mostly, the agents explore locally. Rarely, they take analogical jumps to the corners of an imaginary square — the complete opposite of what they’ve done so far in each dimension. This hedge always results in a slightly lower performance in static times, but it can pay off in spades in a rapidly and unexpectedly changing dynamic environment.

Probability and Possibility in Analogy-Making

The representations we use predispose our lines of inquiry, define the conceptual dimensions we can play with, hint at the directions our imagination and creativity should follow. Our representations of high-level concepts never align perfectly, and so what each of us sees and imagines differs greatly. Some things are incredibly hard to reach from one vantage point yet naturally spill out from another.

Different theories that describe the same thing have different qualities when it comes to change. Some are more robust than others. Some are well-positioned for serendipity, some will fail to see the light if it comes knocking on their head. An explanation that has done somewhat poorly might prove the best way forward in a changing landscape, as a simple natural tweak to it can provide the perfect adaptation. Another that has been generally right so far might require much backtracking to keep pace with even slight shifts in its surroundings.

Analogies have a dual-purpose, they both obstruct our way and push us forward. They limit what we can reach, and by the same token increase our likelihood of hitting on interesting explanations. This is not necessarily a trade-off — if change is constant, and all local options have been exhausted, it makes sense to only attempt large contrarian leaps. We exchange possibility with probability.

Passively or intentionally, analogies drive creativity. Yet those we’ve seen so far do not have any exit hatches from their own fixed borders, no way to escape and discover other analogy spaces that might be more beneficial. For that we need a universal way to express analogies, a way for analogies to talk about and modify themselves.

Self-Modifying Analogies

Just as we can use analogies to explore other possible programs in the analogy space, we can use them to explore other analogy spaces. The key here is to allow the programs to have a say in how they change, to not be totally controlled by the uncertain winds of random mutation. We will do this by introducing a universal structure for defining self-modifying programs. Then, we’ll see how programs can use this system to both intentionally alter their approach and adjust their representations to accommodate serendipity.

In the discussion that follows we’ll talk about programs — agents, processes, models, hypotheses, explanations — as directed acyclic computation graphs. Individually, each program is non-Turing-complete; it’s guaranteed to halt and we’ll be able to tell in advance its time and space complexities. Yet in aggregate, run iteratively and indefinitely, this process can express any Turing-complete computation, and whether it will reach a fixed-point is indeterminate. We use this approach to offer a simple formulation unseasoned by disclaimers. Still, the following construction will get a bit messy and confusing, an unavoidable part of the code-as-data and data-as-code level-mixing inherent in self-reference.

So far, we’ve thought about programs in the usual way: a function that receives an input and produces an output, an agent that receives observations and decides on a course of action, an \(f(x) \rightarrow y\). We now ask of our programs to become self-modifying.

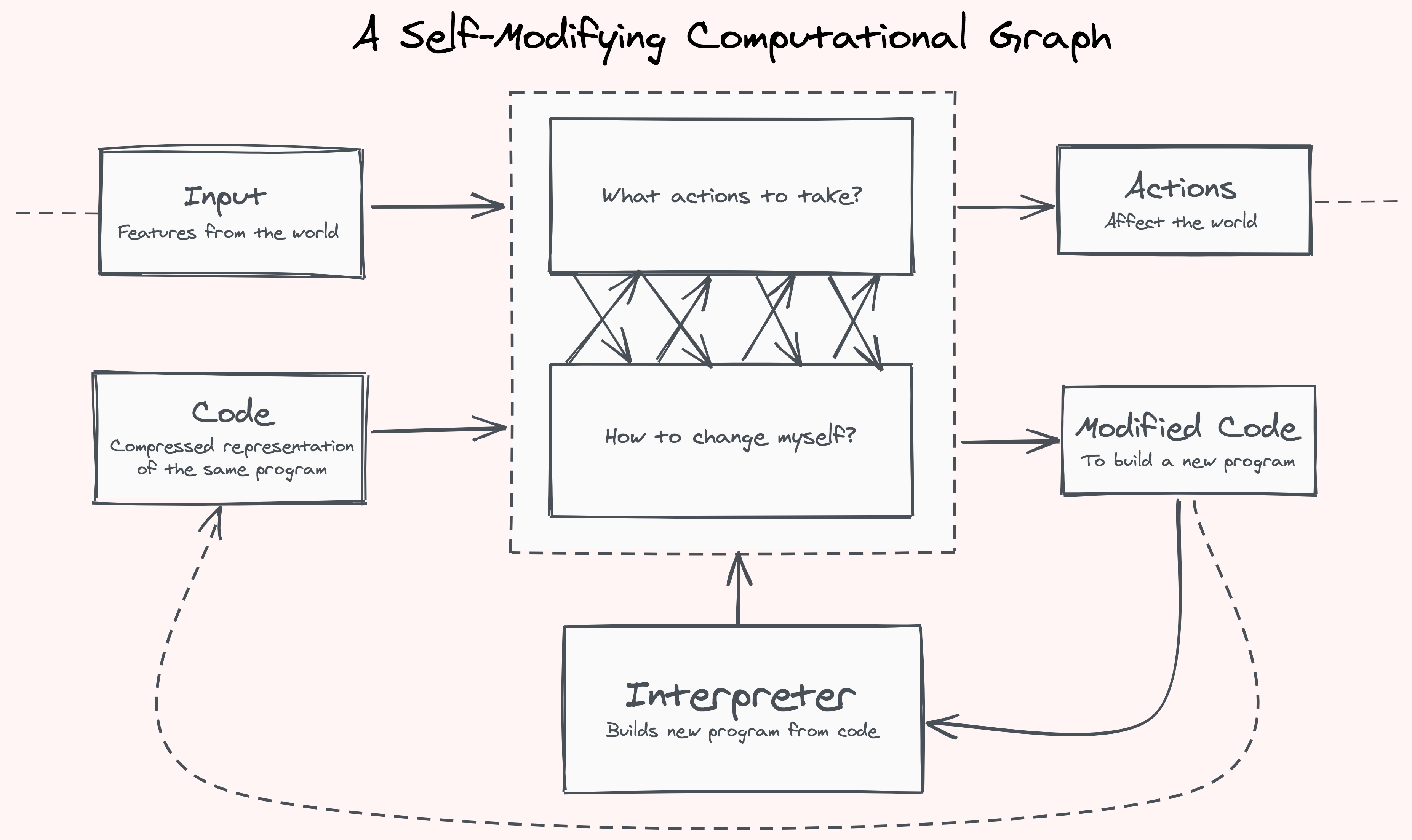
Self-modifying programs must use a compressed representation of themselves, for otherwise they wouldn’t have any space to do something about it. It is impossible for a program to attend to itself in full. The corollary is that a program in an instant cannot actively change itself in every which way, it only has limited avenues available at each point.

To build the compressed representation we’ll need a fixed language \(L\) to describe it. Any language that can universally describe computation graphs would suffice, be it assembly-like, LISP-like, or a self-organized collection of state machines or graph transformation rules. However, any such language is only a way of bootstrapping the process. The universal flexibility of the self-modification structure allows us to move to any other universal language — hopefully one providing more suitable analogy spaces for expressing our current aims — just as evolution has moved to and created many mediums of expression throughout the course of the history of life.

How do we affect change? The ideal candidate to start with is the identity matrix, being a description of perfect self-reproduction. Due to its sparsity and structure it can also be easily compressed. For support, we can also add a vector of bias, so that we can offset as well as amplify. Using these two fundamental structures we can change any part of the compressed representation of the program, including the parts that define how the program changes itself.

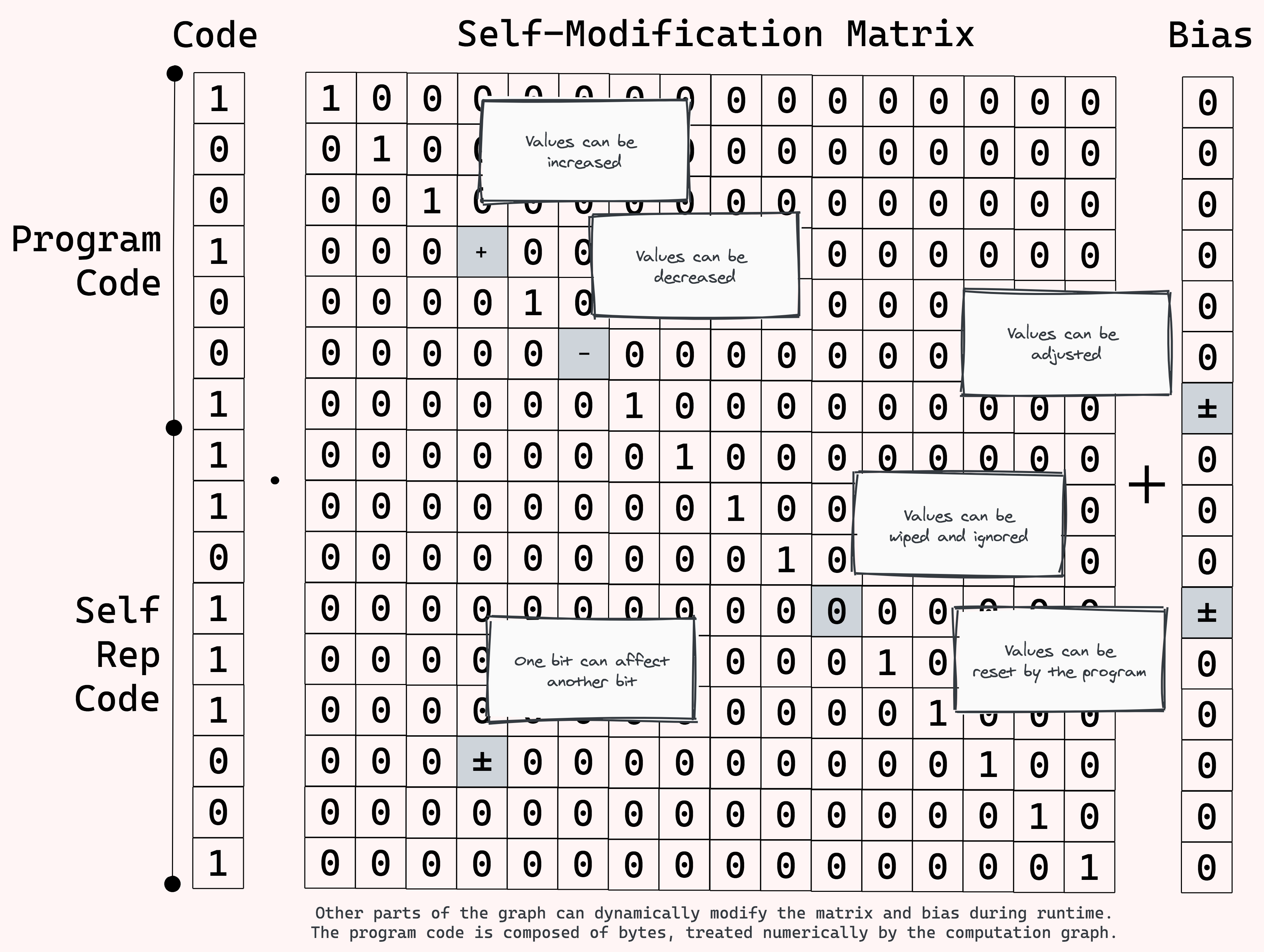
Change can then come from several sources:

1. Phenotype Mutation - As random change to the full unrolled program, equivalent to local optimization in the full state space, little flutters to adjust their position. Some of the mutations at this level, even if proven successful, will not make it to the next generation, as they are not properly reflected in the model’s self-representation.

2. Genotype Mutation - As random change to the compressed code of the program, equivalent to local optimization in the program’s analogy space. This allows the program to passively undergo small variations in their compressed state space that map to far-reaching changes in the full state space. The right medium makes the things we want easy to reach and those we rather avoid hidden away.

3. Intentional Change - As directed change actively taken by the program itself during its execution. The program can change its own compressed code by shifting it with addition, by scaling it with multiplication, or by altogether setting new values instead. This is all done dynamically during the program’s runtime, and can be based conditionally on input from the outside or intermediate computations. As a simple example: if the program finds that some of its nodes equally respond to the same stimuli from the world, it can modify the strength of the connections between them. Or, if a pattern in the world passed some internal check, the program can store it in its self-representation, and use it for further computation in later frames.

We now have all the necessary building blocks to construct self-modifying agents that can explore the search space both locally and globally, in diligent accumulation or by leaps and bounds, intentionally or serendipitously, all using analogies on their self-representation. Putting it all together, the following process appears:

1. Construction: A population of self-modifying agents is generated from an initial blueprint by an interpreter that takes the agents compressed self-representation and builds a computational graph out of it.

2. Program: Each agent’s program is given two inputs: the input observations from the environment and its own compressed self-representation. In return, it has two outputs: the actions to be taken in the environment, and a modified compressed self-representation. In between, data and code can freely pass between these dimensions — the program can consult the input when changing itself, or consult its code to decide on an action.

3. Feedback: The actions of the agents change the environment. A reward signal of each agent’s performance, either synthetic or natural, is collected.

4. Regeneration: A new offspring generation of agents is created based on the rewards, each agent has a probability for its share of offspring based on its performance.

5. Mutation: The offspring generation is created by taking the new self-representation of the agents and employing outside mutation on it. The computational graphs of the offspring generation are built, and the process repeats.

It might be easier to think through it all by seeing it in pseudo-code form:

while True:
	# Build a computation graph from each agent’s code.
	programs = [build_program(agent.code) for agent in agents]
	# Retrieve the observations of the environment each agent receives.
	inputs = [environment.get_observation(agent.id) for agent in agents]
	# Run the agent programs. Each receives its input from the world,
	# and its own compressed self-representation. Each returns actions
	# it wishes to take in the world and a modified self-representation.
	outputs = [program(input, agent.code)
		for program, input, agent in zip(programs, inputs, agents)]
	# Separate the actions and the modified self-representation codes.
	actions, codes = outputs[:,0], outputs[:,1]
	# Update the environment’s state and calculate each agent’s reward.
	rewards = environment.update(actions, agents)
	# Create an offspring generation of agents based on the rewards
	# and the modified self-representation codes.
	agents = offspring(agents, codes, rewards)
	# Outside mutation to the compressed code of the new generation.
	agents = [mutate(agent, probabilities) for agent in agents]

Agents are embodied theories, a self-perpetuating explanation of the world they find themselves in. They do not look for improvement in a void, it is too vast; they start the search for answers from where they are, from what they are. To better their position they change themselves: locally, by looking around them for a slight beneficial change, serendipitously, by shaping themselves in ways favorable to mutation, and intentionally, by modifying themselves based on their current state and their observations of the world.

As a whole, the entire population of agents offers myriad different opinions, stories, and models of the world. Each is acted upon individually, independently, and with conviction. Some stories offer a better vantage on the world. Some are more malleable and fortuitous in disruptive times, spring-loaded to discovery. In times of equilibrium, the agents will tend to converge toward exact automation and perfect execution. In times of change, those who can quickly adapt to the upheaval, by chance or foresight, will shine. Those on the fringe who could see the future would lead the way for the rest.

At any point, analogies allow the agents to break free from their assumptions, to try the complete opposite of any preconceived notions they ever had. Agents can form clear and concise theories, then break them to parts and try out the variations the structure implies. With the universal capability to address themselves and the structures they use, agents are able to not only change themselves, but change the way they change themselves. No single obstacle can stand in their way.

Analogies, even as extensive representations as we can imagine, will have their blindspots. As do we. Any specific model, even all the models in aggregate, will still have uncountably many truths farther than their reach. And yet, they’re adaptive, flexible, and dynamic — any specific target can be had in time.

In contrast, the static optimization methods we use today have permanent blindspots they cannot outmaneuver — someone has to go in to restart the machine. We can dangle a carrot in front of their eyes which they can never reach. Universal Intelligence requires many such carrots to keep the charade going. Fortunately, challenges are not in short supply. Analogies, then, are the least worst way we know of going about things.

Building Creative Machines

This is the foundation of our research program. It is only the start. It took life on Earth three and a half billion years and innumerable parallel processes to get to where we are. To bring our machines to the level of an exceptional human being, let alone groups of people, we must speed things up, and work alongside the agents in the new medium of universal intelligence.

Today, scientific progress in the field of Machine Learning is driven solely by humans. By serendipitous chance and intentional foresight research groups try out many different approaches and ideas for architectures, prior knowledge representations, and optimization techniques. The machines don’t do much machine learning: they simply follow through as an empirical validation mechanism. Some ideas work and get incorporated into the future evolution of the field. Others fail the test of time and are quickly forgotten. The growth and assimilation of knowledge is done by the research community. This is how the scientific method works, and also how intentional evolution works. There is no reason to set them apart.

Metaphor allows us to shift the process of universal intelligence research and development toward an integrated and streamlined paradigm. Our research efforts can now be consolidated directly with the agents ongoing learning, exploration, and discovery.

There is no longer a need to run hundreds of iterations of isolated, ablated, hyper-parameterized and fine-tuned experiments in all their variations against multiple datasets and competing baselines only to, hopefully, get a bolded line in a table saying ‘our model’ and showcasing a 0.32% improvement (in some scenarios. If it reproduces. Thorny issues left for future work).

When researchers are unexpectedly struck by an apple tree, or come running from a warm bath with a strange cry, having just glimpsed a rare and beautiful possibility, they can immediately code and inject their newfound theory, and the structures it entails, into the constantly-running population of live agents, who, meanwhile, never cease trying their own approaches and variations on a theme.

New ideas can be compiled directly into the source code of existing agents. They can be surgically moved around. They can be added to the entire population or only conditionally to some members. They can take effect immediately or recessively lay dormant and wait for the right mutation and setting to pick them up. They can be large-scale logical engines or mere fragments of sensible micro-patterns. Once added, they can be moved, combined, separated, reinterpreted, reparameterized, and have their structures explored. The good ideas will stick. The irrelevant ones will fade.

The agents, using chance, serendipity, and intentional change, will constantly try out new combinations and expressions. The researchers, by the same token, foster them, tending the fire, adding possible priors, heuristics, and meta-learning architectures to the mix as they deem fit.

All of our existing body of work in Deep Learning — any kind of computation, really — can be compiled and introduced to the agents source code. A direct compilation is straightforward, but a more nuanced compiler or an annotating programmer can bring forth potentially explorable and parameterizable compressed representations that will provide the agents with flexibility to play with. The low-level universal language we use to describe self-modifying computation graphs is our compile target — many higher-level languages can be built on top of it. Programmers can lessen their concern for the exactness of their ideas, and focus more on the shape of thoughts they promote.

The Road to Universal Intelligence

Intelligence belongs at the phase transition between the unknown and the automated. It is only where the landscape continuously changes and new problems crop up that it has an overwhelming edge. Universal Intelligence works best in dynamic environments, where change is constant, and the winner takes most: markets, exchanges, cat-and-mouse dynamics, creative generation, and scientific discovery.

Intelligence is neither artificial nor general. It is an emergent universal threshold. One that allows us to follow through and explore not just one static direction of computation, but all of them, and never in a fixed way. Universal Intelligence allows us to strongly assume worldviews that filter and structure our behavior while still maintaining sensible alternative counterfactual avenues for thought, never constraining us to any of the ideas nor their framing.

Many of the limits we consider as human are in fact a fundamental part of our computational universe and our limited observational status within. Any new machine or medium we’ll endow with creativity and thought will be just as fundamentally fallible as us. They might be faster, more resourceful, eyeing paths barely accessible to us, uniquely separate in communication and intuitive style, but in their essence they will be as universally capable as us. Whatever they do, we’ll be able to trace in principle, even if it takes us a hundred times the effort, and whatever they cannot intrinsically reach, so can’t we. But there is plenty, an infinite plenitude, we can.

If a machine is expected to be infallible, it cannot also be intelligent.

— Alan Turing